Allen's Interval Algebra
1600 Words | Approximately 8 Minutes Read | Last Modified on July 9, 2019
A paper by Keith May, Steve Roskams, and James Taylor read at the Computer Applications in Archaeology meeting in Krakow this Spring caught my attention. Titled When Harris Met Allen in the Matrix, the paper indicated the authors' desire to reason about the relations between intervals represented by contexts not related to one another on a line of a Harris matrix. The hope expressed in the paper was that Allen’s interval algebra might provide the tools for this kind of reasoning. Keith and James were both kind enough to discuss their thoughts at some length over food and Polish beer, where they made a case that the Allen algebra is the right tool for the job. Is it?
The Allen algebra identifies an exhaustive set of thirteen basic relations between two definite intervals, each of which is labeled descriptively (fig. 1). Note that the relations in the right column are the converses of the relations in the left column.
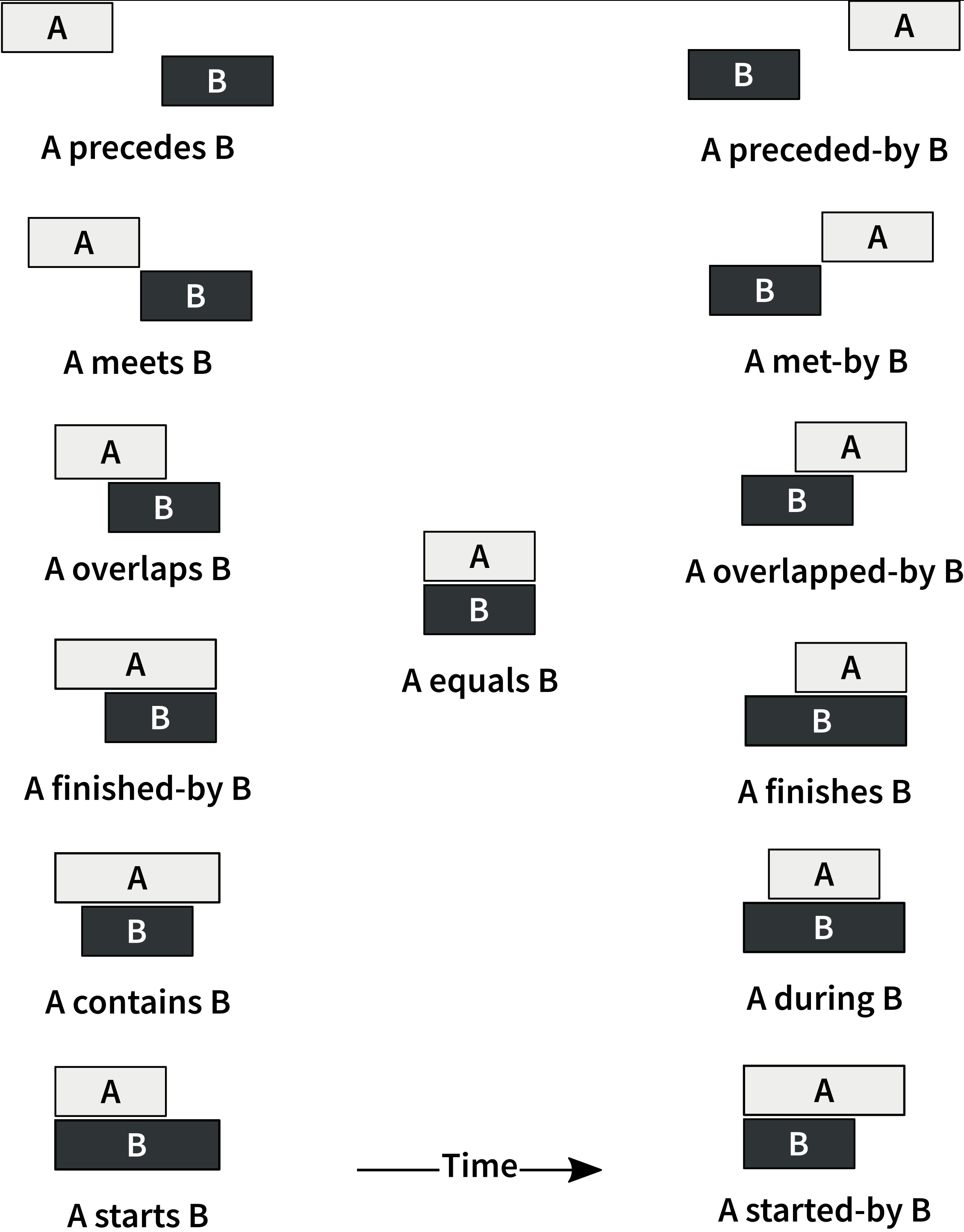
Figure 1: Allen relations of two intervals, A and B, and their descriptive identifiers
There are two kinds of basic relations: concurrent relations overlap one another, and non-concurrent relations do not (fig. 2). This distinction is useful for archaeology because the Harris matrix models non-concurrent relations and has nothing to say about concurrent relations. Concurrent relations are the ones that May, Roskams, and Taylor hope to reason about.
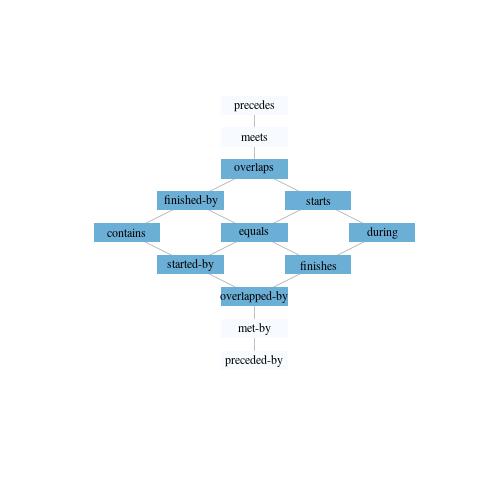
Figure 2: The Allen relations displayed as a lattice in which concurrent relations are shaded dark
May, Roskams, and Taylor are interested in the Allen interval algebra because it includes a composition operation that can be used to infer relations between two intervals that have no direct relationship but are each related to a common interval. So, knowing the Allen relation of intervals A and B and of B and C, but lacking information on the relation of A and C, the composition operation can be given information on the relations between intervals A and B and intervals B and C to yield the strongest possible inference about the relation of intervals A and C.
Here’s one way this might work in archaeology. Given a Bayesian calibration of a chronological model based on a Harris matrix with at least two lines, where interval A corresponds to a dated context on one line and interval B corresponds to a dated context on another line, determine the Allen relation of A and B empirically using the joint posteriors yielded by the calibration. Then, associate interval C with a context on, say, the B line and reason about the relation of intervals A and C by applying the composition operation to the empirical relationship between intervals A and B and the non-concurrent relation between intervals B and C indicated by the Harris matrix. Might this procedure yield a useful result?
An immediate worry is the Allen algebra describes relations between definite intervals with precise endpoints, but the interval estimates yielded by Bayesian calibration are indefinite with endpoints that each range over decades or centuries. Most packages that implement Bayesian inference use a sample based approach. In such sample based approaches each iteration of the sampler produces one internally consistent, plausible set of dates given the data and the a priori stratigraphic information supplied. By comparing results iteration-by-iteration, we can then make statistical statements about relationships for which precise, deterministic statements are not available. Technically speaking, the indefinite intervals produced by this sample based approach are not a problem for Allen’s interval algebra because an indefinite interval can be represented by the set of basic relations realized by the Bayesian sampler. The question is whether or not comparison of indefinite intervals yields a relation set capable of making archaeologically useful inferences. The goal here is to achieve a strong relation set that includes a few basic relations, rather than a weak relation set that includes many basic relations.
Fortunately, I’ve been working with Barry Rolett on a project to incorporate new dating evidence from the stratified Hanamiai site in the Marquesas Islands and to compare the chronology of Hanamiai with the chronologies of two other stratified Marquesan sites at Hane and Hakaea Beach. The chronological model for the project’s Bayesian calibration can be generated from a Harris matrix with three lines, one for each of the sites. The dating evidence collected over a half century has been a challenge to model and calibrate, with issues of in-built age, conflicting estimates of the age of the local marine reservoir, and uncertain charcoal identifications. One calibration among the dozens we’ve run yields indeterminate intervals with endpoints that range over more than a century (fig. 3). Given this challenging situation, is it possible to reason about relations among the archaeological contexts at the three sites using Allen’s interval algebra?
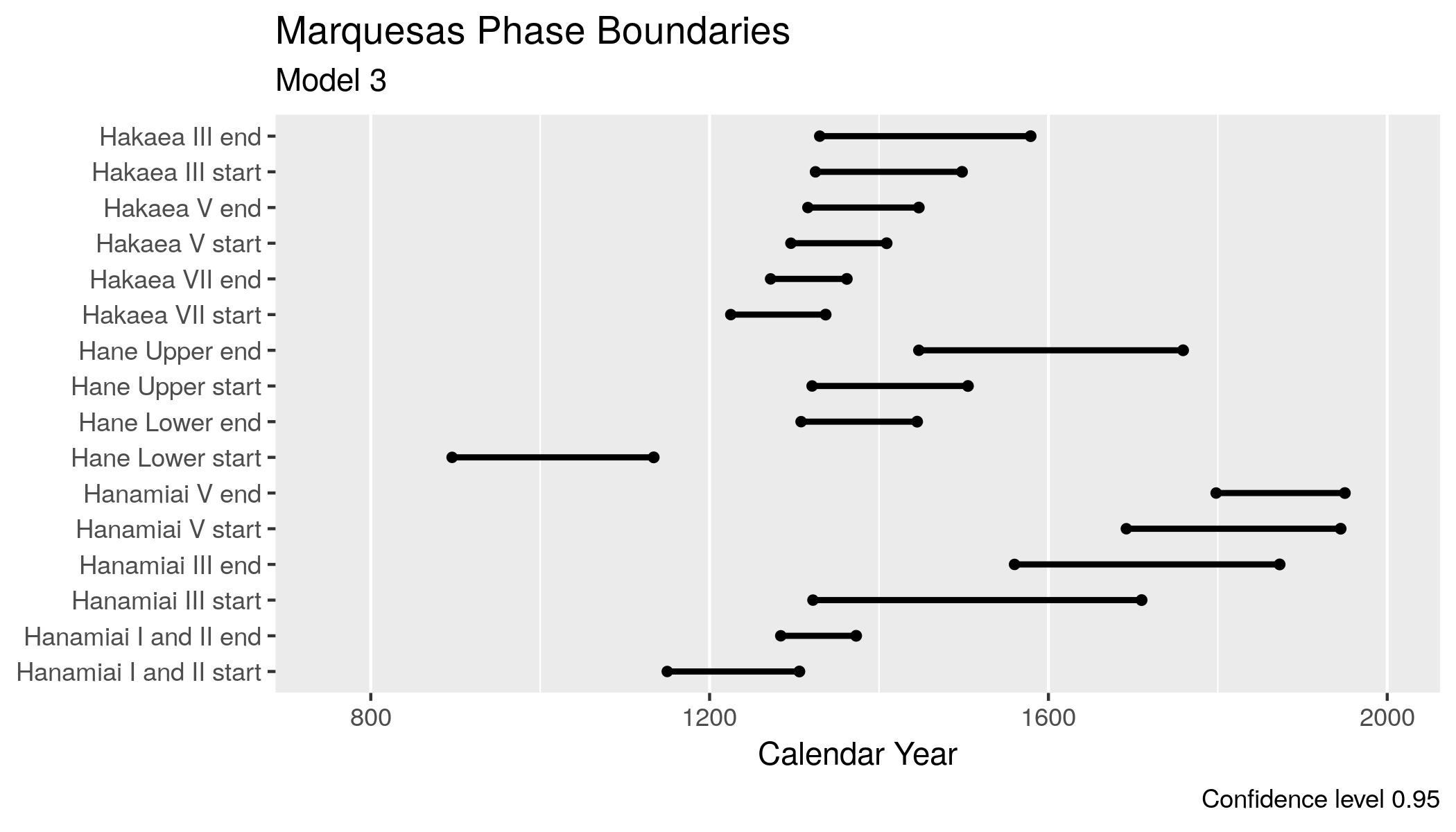
Figure 3: Age estimates for phase boundaries, Marquesas Model 3
I wrote an R function, determine.allen.relation(), to find out. The function
works with the 13 valued algebra or with a six valued algebra that includes only
relations with distinct endpoints (fig.4). Use of the
six valued algebra in the archaeological case is indicated by the fact that
endpoints in a Bayesian calibration rarely coincide; the seven basic relations
with indistinct end points typically make up together a few percent of the
relations observed in a Bayesian calibration of the Marquesan evidence.
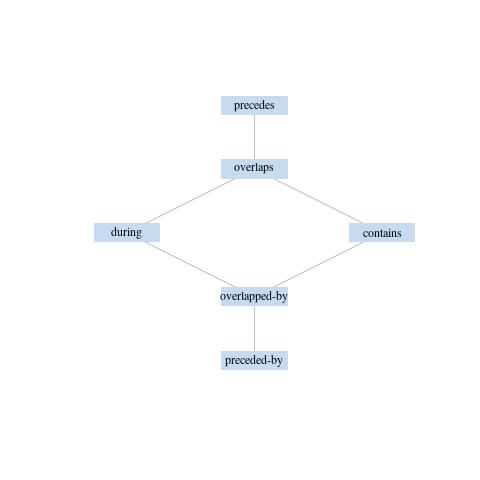
Figure 4: Lattice of the basic relations of a six-valued algebra
When determine.allen.relation() is asked to compare Hanamiai Phases I and II
with Hakaea Layer VII it produces a Nökel lattice (fig.
5). The Nökel lattice indicates in dark blue that the
interval represented by Hanamiai Phases I and II most likely contains or is
overlapped-by the interval represented by Hakaea Layer VII. The figure
also highlights the relations preceded-by and overlaps in a lighter shade of
blue, indicating that these relations are somewhat less likely. The relationship
between the intervals represented by the two contexts is relatively weak, as
indicated by the fact that four nodes of the lattice are rendered blue. A
strong relationship would be indicated by a lattice with a single dark blue node.
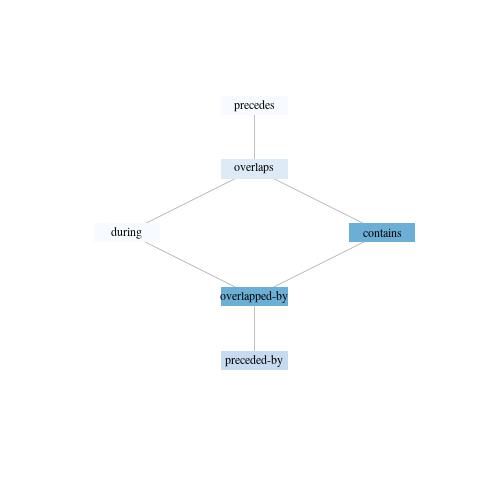
Figure 5: Lattice illustrating the Allen relation set for the indeterminate intervals for Hanamiai Phases I and II and Hakaea Layer VII
The determine.allen.relation() function also returns a list that summarizes
the Allen relation set yielded by the comparison. The first item on the list is
allen.result, which reports the number of times each of the six Allen
relations was observed in the Bayesian calibration. The list item,
allen.proportion, reports the proportion of each basic relation in the whole
in order of decreasing frequency.
$allen.result
p o D d O P
995 5637 102799 5077 100522 15370
$allen.proportion
D O P o d p
0.4462 0.4363 0.0667 0.0245 0.0220 0.0043
In the comparison of Hanamiai Phases I and II and Hakaea Layer VII, the Allen
basic relation set, allen.set, comprises the six relations in the six valued
algebra. This is the weakest possible result, and it indicates that necessary
inference using the Allen algebra is not possible in this situation. This can be
seen in the list item, allen.1.to.precedes.2, which infers the relation
between the first term in the comparison, Hanamiai Phases I and II, and an
archaeological context that precedes the second term in the comparison, Hakaea
Layer VII. As expected, the inference in allen.1.to.precedes.2 comprises the
six relations in the six valued algebra, indicating no inference is possible.
This comparison, specifically chosen for its difficulty, is incapable of
supporting necessary inferences with the Allen algebra. Can a statistical
approach break this impasse?
$allen.set
[1] "p" "o" "D" "d" "O" "P"
$allen.1.to.precedes.2
[1] "p" "o" "D" "d" "O" "P"
The relation set can be strengthened by eliminating basic relations that appear
infrequently in allen.set. The determine-allen-relation() function includes
an argument, threshold, that instructs the function to include only the most
popular relations in the comparison, such that the sum of allen.proportion
equals or exceeds the value passed to threshold. Using the default value of
0.95 for threshold, the function returns the set, allen.uncertain.set, which
comprises four of the basic relations in the six valued algebra. This increase
in strength yielded by the uncertain
relations set makes possible an inference about the relationship between the interval
represented by Hanamiai Phases I and II and the interval represented by the
natural underlying Hakaea Layer VII. This relation, reported in the list item
allen.1.to.precedes.2.uncertain, indicates that the interval represented by
Hanamiai Phases I and II either contains , is overlapped-by, or is
preceded by the interval represented by the natural underlying Hakaea Layer
VII.
$allen.uncertain.set
[1] "D" "O" "P" "o"
$allen.1.to.precedes.2.uncertain
[1] "D" "O" "P"
The inference yielded by the uncertain relations is relatively weak, but it does indicate Allen’s interval algebra is capable of making inferences about the relations of intervals on separate lines of a Harris matrix. In particular, the example shows that the ability to make inferences depends on the strength of the relation sets yielded by the data.
Further inquiry might determine whether or not Allen’s interval algebra will yield stronger inferences when applied to the results of a dating program designed according to modern standards.
